In this post we will be learning about how to use Gamma in options trading and how knowing Gamma of an option helps you to be a much better option trader. There is a very important term which should be known to an option trader termed as Option Greeks.

When it comes to options trading, understanding the greeks – Delta, Gamma, Theta, Vega, and Rho is critical for building effective strategies.

Among these, Gamma plays a pivotal yet often underappreciated role. While Delta garners much of the attention as it measures an option’s sensitivity to price changes in the underlying asset, Gamma acts as the engine that determines how Delta changes in response to those price moves.

This article provides a deep dive into Gamma, its relationship with Delta, its practical applications, and examples to illustrate its significance.

The Option Greeks represent the uniformity of the stock market.

It help us to know how the option will behave to changes in certain variables attached with the pricing of an option contract. Greeks is a term used in the options trading to represent the different dimensions of risk involved if you take any position in option trading.

Before we go in depth in to option Greeks and Gamma I would request you to have Basic understanding of options ,Option moneyness , How to read option chain table and what is Delta in option trading which by the way another option Greek that you should know before understanding Gamma.

By understanding these Options Greeks, traders can make more informed decisions about buying, selling or holding options positions.

Having said that let us now understand deeply what is Gamma of an Option and how it will be enhancing your option trading?

There are majorly four Greeks one should be aware i.e. Delta, Gamma, Vega, Theta.

1. Delta – Delta is the amount an option price (premium) is expected to move based on a 1 rupee change (up or down) in the underlying stock or index.
2. Gamma – It helps in measuring Rate of change of delta.
3. Vega – This calculate rate of change of premium depending up on change in volatility.
4. Theta – It helps in knowing the effect on premium in respect to days or time left for expiry

As of now let us concentrate on Gamma in options.

but before moving straight to Gamma just a brief reminder about delta is necessary so that you can connect the dots.

“Delta is the amount an option price (premium) is expected to move based on a 1 rupee change in the underlying stock”.

In other words Delta of an option helps in Measuring how an options value changes with respect to the change in the underlying.

Most of the beginners in option trading assume that when a stock moves Rs.1, the price of options premium based on that stock will move more than Rs.1.

Always remember the option is a derivative contract, it derives its value from its respective underlying, it can never move faster than the underlying. In reality it does not work like this at all.

This is when we need to be aware of Delta of an option. By knowing this you will be able to find ” how many points will the option premium change for every 1 point change in the underlying.

What Exactly is delta ?

• The delta is a number which fluctuates Between 0 and 1 for a call option, sometime it also referred as 0 to 100 scale. Suppose the delta value of 0.30 on 0 to 1 scale is identical to 30 on the 0 to 100 scale.
• For a put option its ranges Between -1 and 0 or -100 to 0. Similar to Call option the delta value of Put option can be calculated as -0.50 on the -1 to 0 scale is equal to -50 on the -100 to 0 scale .

Few important thing to remember about Delta option Greek:

• Call option lose value when the underlying drops in value. As a result Delta is +ve for call option.
• Call option gains value when the underlying gains in value. As a result Delta is +ve for call option.
• Put option gains value when the underlying drops in value. Delta is -ve for put option.
• Put option loses value when the underlying gains in value. Delta is -ve for put option .
• Expected change in option premium = Option Delta * Points change in underlying
• ATM options have a delta of 0.5
• ITM option have a delta of close to 1
• OTM options have a delta of close to 0
• For put option just use -sign in front
• Put option delta ranges between -1 and 0
• Call option delta ranges between 0 and 1

Also just a reminder to known moneyness of an option :

For Call options :  ITM – ATM – OTM. So all strike below ATM are ITM and all above are OTM.

For Put options  : OTM – ATM – ITM. So all option strikes above ATM are ITM.

You can read more about Delta here

Remember you do not need to calculate delta values manually as it is available with many brokers in built in their trading platform.

and if you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..

now let us comeback to the original topic Gamma and how it will help you to be a better option trader.

 

What Is Gamma In Options Trading?

Gamma measures the rate of change of Delta for every 1 point change in the price of the underlying asset. In other words Gamma of an option helps us to find the corresponding change in the delta of the option with respect to the change in the underlying value.

Delta measures how much an option’s price will change for a 1 point move in the underlying asset. Gamma explains how that Delta itself will change if the underlying asset continues to move.

The underlying value is the price at which the underlying asset such as a stock (SBI), index (Nifty) trades in the spot market. This is current market price at which stock is trading in spot or equity market.

Spot market is the regular equity market, you would see the price difference in spot market and futures price. You might ask why is there difference in prices? Spot prices are for immediate buying and selling, while options contracts delay payment and delivery.

Gamma is mathematically expressed as:

 

 

To find the Gamma of an option, we use a mathematical formula derived from the Black-Scholes Model (or similar pricing models).

Gamma gives traders a deeper insight into how their option positions will react to sudden price movements, particularly in volatile markets.

 

What Is the Value of Gamma and it’s range:

The range of Gamma depends on various factors like the option’s characteristics, volatility, and time to expiration. However, Gamma always lies within certain boundaries:

Typical Gamma Range

Values:

1. Gamma is non-negative and generally peaks around the At-The-Money (ATM) point.
2. It decreases as the option moves deeper In-The-Money (ITM) or further Out-of-The-Money (OTM).

Scale:

1. Gamma values are typically small (e.g., 0.01 to 0.10).
2. They depend on the option’s underlying price and how close it is to the strike price.

 

Factors Affecting Gamma Range

Time to Expiration:

1. Near-expiry options have higher Gamma, especially for ATM options.
2. Gamma decreases as time to expiration increases because Delta changes less rapidly for distant expiries.

Volatility:

1. Higher volatility spreads Gamma across a broader range of prices.
2. Lower volatility concentrates Gamma closer to the ATM price.

 

Examples of Gamma Ranges

Low Gamma:

1. Far OTM options: Gamma ≈ 0.01 or less.
2. Deep ITM options: Gamma ≈ 0.01 or less.

High Gamma:

ATM options nearing expiration: Gamma can reach 0.05 to 0.10 or higher.

 

Gamma In realistic market conditions:

• Gamma values typically range between 0.0 (for far ITM/OTM options) to about 0.1 (for ATM options with short expirations).
• For most retail traders and common scenarios, Gamma usually stays below 0.15.

 

Hence for standard (vanilla) options like calls and puts, Gamma is always positive. This is because Gamma measures how Delta changes as the underlying price moves, and Delta increases for both calls and puts in their respective directions:

1. For Call Options:
   • Delta increases as the underlying price rises (positive correlation). Gamma ensures Delta rises smoothly.
2. For Put Options:
   • Delta increases in magnitude as the underlying price falls (negative correlation). Gamma ensures this change is smooth and predictable.

 

Non-Standard Cases (When Gamma Could Be Negative):

Gamma can turn negative in certain non-standard cases, such as:

Short Options Positions:

If you are short a call or put, you inherit a negative Gamma, meaning your Delta decreases in unfavorable directions. For example:

1. If the underlying price rises sharply and you’re short a call, Delta increases against you.
2. If the underlying price drops sharply and you’re short a put, Delta also moves against you.
3. This is why short positions have higher risk exposure to sharp movements.

Exotic Options:

Some exotic options (like barrier options or options with complex payoffs) may have scenarios where Gamma behaves differently and could turn negative for certain price ranges.

If you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..

 

Let us understand the Gamma range with hypothetical values for ITM, ATM, and OTM options:

Scenario

Assume:

• Strike Price: ₹100.
• Stock Price varies between ₹80 and ₹120.

Gamma behavior is simulated as follows:

• At ₹100 (ATM): Gamma is at its peak because Delta is most sensitive here.
• As the stock price moves ITM (e.g., ₹110, ₹120) or OTM (e.g., ₹90, ₹80), Gamma decreases.

Gamma Range Table:

Stock Price (₹)	Gamma
80 (Deep OTM)	0.01
90 (Near OTM)	0.03
100 (ATM)	0.10
110 (Near ITM)	0.03
120 (Deep ITM)	0.01

 

Explanation:

1. Deep OTM (e.g., ₹80):
   • The option is unlikely to be exercised.
   • Delta changes slowly, so Gamma is near 0.01 (very low).
2. Near OTM (e.g., ₹90):
   • The option starts to gain value, and Delta begins to change faster.
   • Gamma rises to around 0.03.
3. ATM (e.g., ₹100):
   • Delta is most sensitive to changes in the stock price.
   • Gamma peaks at 0.10 (maximum).
4. Near ITM (e.g., ₹110):
   • The option is increasingly ITM; Delta stabilizes near 1.
   • Gamma decreases back to 0.03.
5. Deep ITM (e.g., ₹120):
   • Delta is close to 1 and stable.
   • Gamma drops to a low value, around 0.01.

Key Insights:

• Peak Gamma (0.10): At the strike price (ATM), Gamma is highest.
• Low Gamma (0.01): For Deep ITM and OTM options, Delta is stable, so Gamma is minimal.
• Practical Range: Gamma typically lies between 0.01 and 0.10 in most cases.

 

Basics of Gamma:

1. Highest for At-the-Money (ATM) Options: Gamma peaks when the option is at-the-money (ATM). This is because small changes in the underlying price can quickly alter the probability of the option expiring in the money (ITM) or out of the money (OTM).
2. Lower for In-the-Money (ITM) and Out-of-the-Money (OTM) Options: For deeply ITM or OTM options, the Delta is less sensitive to underlying price changes, resulting in a smaller Gamma.
3. Time Decay Impact: As options approach expiration, Gamma increases for ATM options. This phenomenon, often called Gamma risk, makes it challenging to manage positions near expiry.
4. Symmetry: Gamma is positive for both call and put options. It ensures that Delta moves predictably in response to changes in the underlying, regardless of the option type.

If you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..

 

Gamma Vs Delta:

Let us understand Gamma and it’s relation with Delta through a Car analogy:

Imagine Delta as a car’s speed and Gamma as the acceleration:

• Delta tells you how fast the car (option price) is moving.
• Gamma tells you how quickly that speed (Delta) is changing.

Suppose you are driving on a road:

• Delta is your current speed.
• Gamma represents how hard you’re pressing the accelerator or brake. A slight touch (high Gamma) can cause a big speed change.

Let’s break down the relationship between Gamma and Delta using a simple car example.

Imagine a car is traveling on a long, curvy road. The car’s movement represents the changing price of an option premium, and the driver’s actions are influenced by Delta and Gamma:

Position (Distance Traveled):

• The total distance the car has traveled represents the option premium. It increases as the car moves forward.

Speed (Velocity):

• The car’s speed represents Delta, which is how fast the position (distance) is changing.

Acceleration:

• The car’s acceleration represents Gamma, which is how fast the speed (Delta) is changing.

At the Start (Flat Road, Low Gamma):

1. The car starts from rest (Speed=0).
2. Initially, the driver applies constant acceleration (moderate Gamma). This causes the car to gain speed steadily over time.
3. The position (distance traveled or the option premium) starts to increase as the car moves.

 

On a Steep Curve (High Gamma Zone):

1. As the car approaches a sharp curve in the road, the driver must adjust the speed more aggressively.
2. Here, Gamma is high, meaning small adjustments to the car’s acceleration cause noticeable changes in its speed (Delta).
3. Similarly, for an option, Gamma is highest when the price of the underlying asset is near the strike price (ATM). A small movement in the underlying price causes Delta to change rapidly.

 

On a Straight Stretch of Road (Low Gamma):

1. Once the car is on a straight stretch of road, the driver doesn’t need to change the acceleration as much. The car travels smoothly at a more stable speed.
2. Here, Gamma is low, meaning the speed (Delta) doesn’t change much. This is similar to an option that is deep ITM or OTM, where Delta becomes stable.

Car Scenario	Option Term	Explanation
Car’s position (distance)	Option premium	The overall result, showing how far the car has traveled or the option’s value.
Car’s speed (velocity)	Delta	The rate at which the car covers distance, like how fast the premium changes.
Car’s acceleration	Gamma	The rate at which speed changes, like how fast Delta adjusts to price changes.

 

Gamma controls Delta, just like acceleration controls speed. When Gamma is high (near ATM), the car’s speed (Delta) changes quickly with even a small press on the gas pedal.

Far from the curve (deep ITM or OTM), Gamma is low and the car moves more steadily, requiring fewer adjustments to the speed.

Let us understand Gamm vs Delta through an stock market example now:

Example:

Stock: Infosys (₹1400)

An ATM call with a Delta of 0.5 and Gamma of 0.04.

Infosys rises to ₹1401

Change in delta = Gamma * Change in underlying (0.04*1) = 0.04

New Delta = Old Delta + Change in Delta (0.5+0.04)=0.54

similarly if Infosys drops to ₹1399 → Delta becomes 0.46.

let us take another example :

• Stock Price: ₹100
• Option Type: Call Option (ATM)
• Delta: 0.50
• Gamma: 0.05

Stock Price Moves to ₹101:

• New Delta = $=0.55$

Stock Price Moves to ₹102:

• New Delta = $=0.60$

As the stock price rises, Delta increases, indicating the option becomes more sensitive to further price moves. This rapid change in Delta is driven by Gamma.

Aspect	Delta	Gamma
What it Measures	Change in option price per ₹1 move.	Change in Delta per ₹1 move.
Behavior	High for ITM options.	High for ATM options.
Risk Management	Helps hedge directional risk.	Helps manage changes in directional risk.

 

If you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..

 

Drawing Parallels to Options Trading (NIFTY 50 Example):

Now, let’s relate the car’s journey to how options on the NIFTY 50 index behave:

Stage 1 (Price near OTM levels):

1. The NIFTY 50 index starts near a level where the option is out of the money (OTM).
2. Option Premium: The option premium begins to increase as the index price moves toward the strike price.
3. Delta: Delta starts low because the option is far from being ITM, and small changes in the index price don’t affect the premium much.
4. Gamma: Gamma is present but not very high since Delta is changing gradually.

Stage 2 (Price near ATM levels):

1. The NIFTY 50 index moves closer to the strike price, entering the at the money (ATM) region.
2. Option Premium: The premium increases rapidly as the probability of the option expiring ITM rises sharply.
3. Delta: Delta grows significantly, reflecting a rapid increase in the premium’s sensitivity to index price changes.
4. Gamma: Gamma is highest near ATM because Delta is changing quickly with small movements in the NIFTY 50 index.

 

Graphical Understanding of Gamma:

Gamma is highest when an option is At-The-Money (ATM), meaning the stock price is close to the strike price. It decreases as the option moves deeper In-The-Money (ITM) or further Out-of-The-Money (OTM).

Checkout the graph of Gamma Vs Nifty50 below:

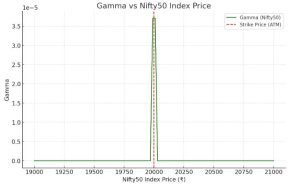
The graph above illustrates Gamma vs Nifty50 Index Price:

• Gamma Peaks at ATM (₹20,000): Gamma is highest when the Nifty50 index price is at the strike price (₹20,000). This represents the At-The-Money (ATM) scenario, where Delta is most sensitive to price changes.
• Gamma Decreases for ITM and OTM Options:
• On the left (Nifty50 < ₹20,000), Gamma reduces as the option becomes Deep-In-The-Money (ITM).
• On the right (Nifty50 > ₹20,000), Gamma reduces as the option moves further Out-of-The-Money (OTM).

This behavior is consistent with options theory and highlights the sensitivity of Gamma near ATM levels for hedging strategies.

 

Examples to explain the impact of Delta and Gamma on the Option Price:

Scenario Setup:

• Underlying Asset: Stock ABC
• Current Stock Price: ₹100
• Option Strike Price: ₹100 (ATM)
• Option Type: Call Option
• Delta: 0.50 (ATM options have a Delta of approximately 0.5).
• Gamma: 0.05

Change in Stock Price:

Suppose the stock price rises by ₹1 to ₹101:

• New Delta = Old Delta + Gamma × Change in Stock Price
• New Delta = $=0.55$

The Delta has increased to 0.55, meaning the option price will now move ₹0.55 for every ₹1 change in the stock price.

If the stock price moves another ₹1 to ₹102:

• New Delta = $=0.60$

The Delta has now increased further to 0.60.

Now let’s assume the option price (premium) was ₹5 initially.

Here’s how the price changes with Delta and Gamma:

1. Stock Price at ₹101:
   • Option Price Change = Delta × Change in Stock Price
   • Option Price Change = $₹0.50$
   • New Option Price = ₹5 + ₹0.50 = ₹5.50
2. Stock Price at ₹102:
   • Option Price Change = $₹0.55$
   • New Option Price = ₹5.50 + ₹0.55 = ₹6.05

Example 1: High Gamma Scenario

You own a Call Option on Reliance Industries Limited (RIL).

• Current stock price: ₹2,400
• Strike price: ₹2,500
• Delta: 0.3 (implying the option price increases ₹0.30 for every ₹1 rise in the stock price)
• Gamma: 0.05

Now, if RIL’s stock price rises by ₹10:

1. Delta will increase by gamma (Γ)×Change in Stock Price=0.05×10=0.5
2. The new Delta becomes 0.3+0.5=0.8

Your option is now far more sensitive to stock price changes!

Example 2: Low Gamma Scenario

For the same RIL call option but with Gamma of 0.01:

1. Delta changes by $=0.1$.
2. New Delta: 0.3+0.1=0.4

In this case, Delta adjusts more conservatively.

Let’s use a Nifty 50 ATM call option expiring in 7 days.

1. Initial Conditions:
   • Nifty 50 Index: ₹18,000
   • ATM Call Option Price: ₹120
   • Delta: 0.5
   • Gamma: 0.03
2. Scenario:
   • Nifty rises to ₹18,010 → Delta increases to 0.53 (Gamma causes Delta to grow).
   • Nifty falls to ₹17,990 → Delta decreases to 0.47 (Gamma causes Delta to drop).

Key Takeaway:

Gamma amplifies the impact on Delta, influencing how your options strategy performs.

If you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..

 

Practical Examples of Gamma in Real Trading:

Let’s explore a few scenarios to see how Gamma works in practice.

Example 1: ATM Call Option Near Expiry

• Stock Price: ₹100
• Strike Price: ₹100 (ATM)
• Option Premium: ₹5
• Delta: 0.50
• Gamma: 0.15

Stock Price Increases to ₹101:

1. New Delta = Old Delta + Gamma × Change in Stock Price 0.50+(0.15×1)=0.65
2. New Option Price = premium + (delta*change in underlying) ₹5+(0.65×1)=₹5.65

Stock Price Increases to ₹102:

1. New Delta = $0.80$
2. New Option Price = ₹5.65+(0.80×1)=₹6.45

As Gamma is high, the Delta changes significantly with each ₹1 move, resulting in larger option price changes.

 

Example 2: OTM Put Option

• Stock Price: ₹105
• Strike Price: ₹100 (OTM)
• Option Premium: ₹2
• Delta: -0.10
• Gamma: 0.02

The negative sign in front of delta value is because it’s put option, keep in mind

• Put option gains value when the underlying drops in value. Delta is -ve for put option.
• Put option loses value when the underlying gains in value. Delta is -ve for put option .

Stock Price Decreases to ₹104:

1. New Delta = Old Delta + Gamma × Change in Stock Price $-0.08$
2. New Option Price = premium + (delta*change in underlying) ₹2+(−0.08×1)=₹1.92

Stock Price Decreases to ₹103:

1. New Delta = $-0.06$
2. New Option Price = ₹1.92+(−0.06×1)=₹1.86

For OTM options, Gamma is low, resulting in smaller changes in Delta and the option price.

 

Impact of Gamma on Different Strike Prices:

Gamma varies across the moneyness spectrum of options:

At-the-Money (ATM):

• Gamma is highest for ATM options.
• Delta changes rapidly as the underlying price moves.
• Best suited for short-term, high-volatility strategies.

In-the-Money (ITM):

• Gamma is lower for ITM options.
• Delta is more stable and closer to 1 (call options) or -1 (put options).
• Ideal for directional strategies with moderate risk.

Out-of-the-Money (OTM):

• Gamma is also low for OTM options.
• Delta changes slowly, and the probability of the option expiring ITM is lower.
• Suited for speculative trades with lower premiums but higher risk.

 

The choice of strike price depends on your trading objective, now let us understand the different strategies based on Gamma.

1. For Volatility Based Strategies

If you expect significant price movement in the underlying asset:

• Choose ATM Options: High Gamma ensures that Delta changes rapidly, amplifying gains as the price moves in your favor.
• Example: A trader expects a ₹10 upward move in a stock priced at ₹100. Buying an ATM call option ensures rapid Delta growth, leading to larger profits.

 

2. For Directional Bets with Moderate Risk

If you are moderately bullish or bearish and expect smaller price movements:

• Choose Slightly ITM Options: Lower Gamma and higher Delta ensure stable price changes in the option. The option price will still react significantly to price movements in the underlying.
• Example: A trader buys a ₹95 strike call option when the stock is priced at ₹100. Lower Gamma reduces risk from small unfavorable price movements.

 

3. For Speculative Trades with Limited Capital

If you have a limited budget and want to speculate on significant price moves:

• Choose OTM Options: Low Gamma and low premiums offer a cheaper way to bet on large price movements.
• Example: A trader buys a ₹105 strike call option for ₹100 stock. If the stock rises significantly, the low-cost option can yield outsized returns.

 

How To Use Gamma for Timing Your Trades?

1. Near Expiration

• Gamma for ATM options increases as expiration approaches, leading to rapid changes in Delta. If you expect high volatility in the short term, ATM options near expiry are ideal.
• Caution: High Gamma means higher risk. Small price moves can drastically change Delta, affecting both profits and losses.

2. Long-Dated Options

• Gamma is lower for long-dated options, even for ATM strikes. These options are less sensitive to immediate price moves, making them suitable for longer-term strategies.

 

Gamma’s Interaction with Vega and Theta:

1. Gamma and Vega

• High Gamma options (ATM) are also sensitive to changes in volatility (Vega).
• Choose high Gamma options if you expect both significant price moves and volatility increases.

2. Gamma and Theta

• High Gamma options have higher Theta decay, especially near expiration.
• If you cannot monitor positions closely, avoid ATM options near expiry to reduce the risk of rapid time decay.

Gamma and Theta are closely connected:

• Gamma is high for ATM options, meaning Delta changes rapidly.
• Theta (time decay) is also high for ATM options, meaning the option’s value erodes faster as expiration nears.

Example:

You own an HDFC Bank ATM Call Option with:

• Stock Price: ₹1,650
• Strike Price: ₹1,650
• Gamma: 0.1
• Theta: -₹2 per day.

If HDFC Bank’s stock price rises ₹10:

1. Delta adjusts significantly (thanks to high Gamma).
2. Option value increases, but Theta decay erodes gains daily.

 

Practical application of Gamma while trading options:

• If  You hold a portfolio of ATM options.
• Observation: Gamma is high, making your portfolio very sensitive to price movements.
• Action: Reduce exposure by hedging (e.g., buying or selling underlying shares to stabilize Delta).

Hedging Gamma Risk:

Hedging Gamma requires adjusting your position frequently to neutralize the impact of Delta changes. This strategy, known as Gamma Scalping, involves:

1. Monitoring Delta closely.
2. Buying or selling the underlying stock to offset Delta adjustments.

Gamma and Volatility

Gamma reacts differently to changes in implied volatility:

• High Volatility: Lowers Gamma because large price swings make Delta smoother.
• Low Volatility: Increases Gamma because smaller price movements create sharp Delta changes.

Example:

Consider SBI Call Option:

• Strike Price: ₹500
• Stock Price: ₹500 (ATM)
• Gamma: 0.08

If market volatility drops:

• Gamma increases, and Delta changes sharply for small price movements.

If you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..

 

Example of Strike Selection Using Gamma:

Scenario:

• Underlying Asset: Stock trading at ₹100.
• Trading Objective: Exploit expected volatility due to an earnings announcement.
• Option Premiums:
  • ₹95 Strike (ITM Call): Premium ₹7, Delta 0.70, Gamma 0.05.
  • ₹100 Strike (ATM Call): Premium ₹4, Delta 0.50, Gamma 0.10.
  • ₹105 Strike (OTM Call): Premium ₹2, Delta 0.30, Gamma 0.04.

Analysis:

1. ITM Call (₹95 Strike):
   • Lower Gamma means Delta is stable.
   • Suitable for directional trades with moderate risk and capital to invest in higher premiums.
2. ATM Call (₹100 Strike):
   • High Gamma offers greater sensitivity to price changes.
   • Ideal for short-term trades where volatility is expected to increase.
3. OTM Call (₹105 Strike):
   • Low Gamma and low premium mean limited sensitivity to price changes unless the stock moves significantly.
   • Suitable for speculative trades with low upfront costs.

Decision:

• If expecting moderate price movement, choose ITM or ATM strikes.
• For aggressive bets on significant volatility, choose ATM or slightly OTM strikes.

 

Few Tips for Using Gamma in Trading:

Monitor Gamma Risk Near Expiry:

Be cautious when trading ATM options close to expiration, as high Gamma can lead to rapid changes in Delta.

Combine Gamma with Vega:

Use Gamma in conjunction with Vega to manage risks associated with both price movements and changes in volatility.

Avoid Over-Hedging:

Frequent hedging in high Gamma scenarios can lead to excessive transaction costs. Balance the need for adjustments with cost considerations.

Use Gamma to Your Advantage:

Long Gamma positions (e.g., buying options) benefit from large price movements, while short Gamma positions (e.g., selling options) perform well in stable markets.

Key Points for Beginners:

1. Start with Delta: Focus on how Delta impacts your position before diving into Gamma.
2. Track ATM Options: Gamma is most relevant for ATM positions.
3. Practice Hedging: Use mock portfolios to simulate Gamma hedging.

Always keep in mind that

High Gamma = High Risk

Options with high Gamma are sensitive hence traders must manage risk carefully.

If you are looking for the best stockbroker for option trading I would recommend you to checkout this broker, or you can directly use the below link to open the account free of cost.

Open Best Free Trading/Demat/Mutual Fund account online within minutes and start investing and trading in stocks, FNO, Commodity, Currency, ETF, SGB, IPO, Gold, SIP and many more Products..